単位をつけて式を書くと算・理は強くなる?~ディメンジョン思考

「3次元」のことを「3D(3 dimensionの略)」と言ったりするので、「次元」という概念は何となく解っているとは思うのですが、ここではそれとちょっと違う「物理量のディメンジョン」について書きたいと思います。
Table of Contents
算数の答えは本来「値」と「単位」でデキている
昨今の塾のテストなどでは、おそらく効率的に大量採点するために、式を書かせることがあまりありません。
しかも、答えの欄にあらかじめ単位が書いてあることがほとんどなんです。
こんな具合に。
算数に限らず理科の計算問題も同様に、答案用紙に数値を書くだけ、という様式になっています。
しかし、数値と単位両方が揃って「答」なのであって、本来なら両方とも受験生に書かせるのが普通です。
少なくとも私はそう思います。
まあ、上位難関校を除くと、本番の入試でさえプロセスを書かせない学校も多いので、仕方ない傾向かも知れませんが、これでは、単位を気にしながら問題を解く習慣がつくとは、到底思えません。
そういう副作用というかよくない側面も含め、業界?の悪しき習慣だと思うのですが、天に唾吐いても仕方ないので、せめて、自分が解く時ぐらい単位を明記する癖をつけたらいいのにな、と思うのです。
私も、子どもに指導する時、「それって単位は何だっけ」とか言って、極力単位を意識させるようにしています。
しかしながら、試験中に一刻でも惜しいお子さんも(親御さんも)多いことと思います。
単位を意識する効用について、その理由を述べたいと思います。
単位を意識する効用
それはズバリ、イージーなミスが激減することです。
私が受けた共通一次試験(年がばれますね)の物理の問題では、答えが4択だったりしましたが、「ディメンジョンチェックだけで8割方点が獲れる」という噂がありました。
どういうことかというと、例えば振子の周期は
T = 2 π √lg
が正解なのですが、周期の単位は「時間」[s(=秒)]なので、長さl[kg]と重力加速度g[kg/s2]の積の平方根で合っていそうですよね、ということなんですよ。
つまり、単位のチェックだけで他の選択肢が「絶対に正解でない!」と解ってしまうので、値を計算せずとも正解を消去法で選べてしまうのです。
本末転倒とは言え、これってすごいことではないですか?(苦笑)
まあ、共通一次試験のハナシ自体は笑い話なのですが、私でも、何か式が間違っているような気がするとき、掛け忘れや割り忘れをチェックするために、各項の次元が一致しているかを、よく確認します。
というか、基本動作として、だいたいやっています。
要は、次元の違うものを足したり引いたりしていないか? イコールの左右で次元が違ったりしてないか? ということを確認する訳です。
この作業は、「次元解析」とか「ディメンジョン・チェック」と呼ばれます。
大した作業ではありませんが、名前だけはかっこいいですよね!
ディメンジョンとは何か?
順序が前後しましたが、今一度「ディメンジョン」を定義しておきましょう。
ディメンジョンとは、物理量の種類を指定するもの
です。どういうことか説明します。
物理量は、基本的な量どうしを掛け合わせたり割ったりすることで作られます。
微分も微小量同士というだけで割り算の一種ですし、積分も同様に掛け算の一種ですから、どんな量の単位であっても、基本的な量同士の積や商の形で表すことができますね。
これは、単位を使って表してもいいのですが、より一般的に、アルファベット一文字を使って表すのが通例です。具体的には、質量(Mass)、長さ(Length)、時間(Time)それぞれの頭文字の MLT の組み合わせで表します。
例えば、加速度は LT-2 の形で表され、力は MLT-2 の形で表されます。
ニュートンの運動方程式は F=m×a ですが、力と加速度は比例して、その比例定数が質量なのだ、ということがこのディメンジョン標記だけで明らかになりますね。
もちろん、
F [N]=m[kg]×a[m/s2]
と実際の単位で書いても(N=kg・m/s2なので)いいのですが、
MLT-2 = M × LT-2
と書けば、「より一般的ですね」ということです。
つまり、クドクド説明しましたが、ディメンジョン=次元とは、単位の一般的概念、とでも理解していただければいいと思います。
せっかくの機会ですので、代表的な物理量(主に力学)の次元と単位を、一覧にしておきます。
これを眺めているだけで、物理が解ったような気になります(笑)
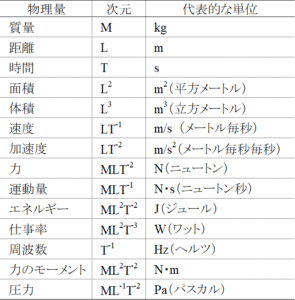
より深い物理の理解と抽象思考のために
前述のとおり、単位を気にしながら勉強すれば、先ずイージーミスが減ります。
別エントリーでも書いたとおり、イージーミスは長い人生の間その子に相当「損」をさせることになるので、そういう悪習は小学生の頃から断った方が賢明です。
また、単位を意識することで、物理に対する理解は格段に深まります。
「数学で習った微積分の知識が、物理(特に力学)の世界の扉を大きく開けてくれた!」というのは、物理を勉強した理系人間共通の感覚だと思いますが、その先駆けともいえるのが、単位による物理量の理解です。
シンプルなディメンジョン思考は、各物理量のつながりを大きく体系的に捉えることに、大いに役立ちます。
またひいては、この感覚は、抽象思考の手助けにもなってくれます。
一人でも多くのお子さんが、面倒草がらずに、単位を意識した学習を小学生の家から実践してほしいものです。


