できない大人も多い「抜け漏れなくダブりなく」~MECE思考

算数が得意なお子さんでも、結構苦手意識があったりする「場合の数」について、考察しながら対策を考えてみたいと思います。
Table of Contents
いつまでたってもできるようにならない「場合の数」
6年生も大詰め。受験直前の12月とか1月になっても、
どうも『場合の数』の得点が安定しない
と悩んだり嘆いたりするお子さんは、実に多いです。
塾のカリキュラムでも他の単元ほど繰り返し登場しないし、ものすごく出題される単元という訳でもないので、過去問など演習でも手を抜きがち、ということかも知れませんが、本質的に得点するのが難しい要因が別のトコロにあるような気がします。
「場合の数」の問題を解くには、多段階のプロセスを、それぞれ正確にこなす必要があります。
具体的には、
- 可能性を「抜け漏れなくダブりなく」考えることができる
- 条件の場合分けを視覚化しながら、確実に「抜け漏れなくダブりなく」数えることができる
- 数えられないような場合は、適当なモデルに従って、正確に計算できる
という多段階の脳を使わねばならず、非常に応用的だといえます。
特にこの中でも「抜け漏れなくダブりなく」というところが鍵となります。
ロジカルシンキングの基本MECE
この「抜け漏れなくダブりなく」という概念の理解は、とても重要です。
英語ではMECE(ミーシー、Mutually Exclusive, Collectively Exhaustive 「相互に排他的な項目による完全な全体集合」)と言われ、もともと米コンサルティング・ファームによって開発された概念で、ロジカルシンキング の基礎のひとつでもあります。
平たく言えば、これを理解していない大人は仕事もできない、という基本スキルです。
例えば、人間という集合を例にとると、
- 年齢による分類は、重複なく網羅できるため、MECEと言える
- 職業による分類は、兼業者や無職もいるため、MECEではない
ということになります。
解き方を如何に「間違いにくいルーティン」に落とし込むか
場合の数に応用して言うならば、例えば
0~5の数が書かれた6枚のカードの中から、3枚を選んで3桁の整数を作ると、全部で何とおりできるか?
とうような問題では、出来る数を、102、103..というように昇順に並べれば、絶対にMECE(重複なく網羅できる)ですから、そういう習慣を身につけているか? というハナシになります。
よく、塾などでの指導でも「樹形図を書きましょう」というような、テクニックと言うか、理由を説明せずに方法だけを刷り込むことがしばしば起こりますが、これでは「必ず重複なく網羅できるか?」という観点での説明が、不十分ですね。
数字を並べる問題であれば「樹形図を昇順で書く」とか、アルファベットを並べる問題では「樹形図を辞書の順番で書く」というトコロまで、丁寧に解説することが必要ですね。
つまり、気がついた順に書き出したりするとMECEでなく失敗するのがオチなので、正しいMECEの手順で解くことを自分でルールにしてしまいなさい、ということなのです。
「1対1」対応とモデル化
前項の解説で、「MECEさえ気をつければ場合の数は解ける!」かのように感じたかもしれませんが、残念ながら事態はそれほど単純ではありません。
MECEは必要条件ではありますが、十分条件ではないのです
(必要条件/十分条件の解説は、別の機会にしましょう)。
場合の数では、ちょっとしたセンスが求められる問題も多くあります。
「センス」という抽象的な表現では解りにくければ、「モデル化とか1対1対応など」と言い換えてもいいのですが、こういった「高度な抽象化」が必要になるケースもしばしばあります。
例えば、有名なこういう問題。
[問題1]
80チームが参加した野球大会で、負けたら終わりのノックアウト方式のトーナメント戦を行いました。
全部で何試合行われましたか。ただし、引き分け試合はなかったものとします。
あなたも既に、答えをご存知かもしれませんね。
1試合終わる毎に、敗退チームが1チームづつ増えていくのですから、優勝チーム(一度も負けないチーム)を決めるまでに、79の敗退チームを生み出せばいいのです。
ですから答えは、79試合。
気がつきましたか?
訊かれているのは「試合数」ですが、考えたのは「敗退チーム数」でした。
つまり、「試合数」と「敗退チーム数」は「1対1」対応しているからこそ、「敗退チーム数」を考えて「試合数」が導かれた訳です。
では、次の問題は如何でしょう。
少し難しいですけれど、考えてみてください。
[問題2]
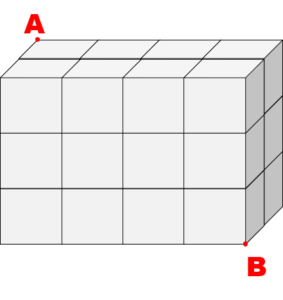
図のように、小さな立方体を24個積み重ねて、直方体をつくりました。
点Aから点Bまで串を突き通すと、何個の立方体を貫くでしょうか。
まず、「2×3×4の直方体の頂点AB間に予め串を通しておいた」と仮定し、その後この直方体を「上から見て縦方向に3回、上から見て横方向に1回、水平に2回切って、立方体に分ける」と考えます。
つまり、「切ってある豆腐を積み上げた直方体に串をうつ」のではなく、「直方体に予め通しておいた串を豆腐と一緒に切る」のです。
何故そんなことを考えるかというと、串が貫く立方体を直接数えるより、分断される串の断片を数える方がずっと考え易いからです。
では具体的に、串はいくつに分断されるでしょうか。
- 縦に3回切ると,ABは3ヶ所で切断される
- 横に1回切ると,ABは1ヶ所で切断される
- 水平に2回切ると,ABは2ヶ所で切断される
それぞれの切断は、ABを何等分かすることになります。
ですから、ABの長さを1としてそれぞれの切断点の位置をAからの長さで表してみると、こうなります。
- 縦に切ると、ABは、1/4、2/4(=1/2)、3/4で切断される
- 横に切ると、ABは、1/2で切断される
- 水平に切ると、
これらの6個に、同じ位置の点があります。2/4と1/2です。
ですから、串は異なる5ヶ所で切断され、6個の断片に分かれることになります。
この「6個の断片」は串が貫いた立方体に「1対1」対応する(断片1つに対し立方体の豆腐が「1対1」対応する)ので、この串が貫く小立方体の数も6個です。
この問題は、3次元で考えるより、1次元(線分)で考えることによって、非常にスッキリ解けることのできる好例です。
では、この問題はどうでしょう。
[問題3]
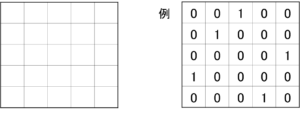
下の図の25個のマス目に、0または1を書き入れます。
例のように、縦に加えても、横に加えても、それぞれ和が1になるようにする書き方は、全部で何通りありますか。
これも、このままでは考えにくいので、ちょっとした置き換えをしてみます。
先ず、マス目に名前(数学的には「座標」と言ってもいいかもしれません)をつけます。
こんな具合です。
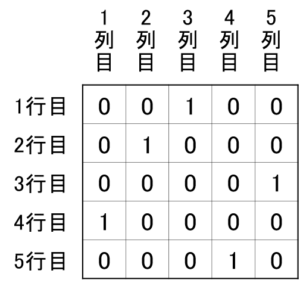
例は、「1列目に1を書くのは4行目、2列目に1を書くのは1行目...」と表現することができます。
ここで、「何行目に1を書くか」を1列目から順に並べると、下のようになりますね。
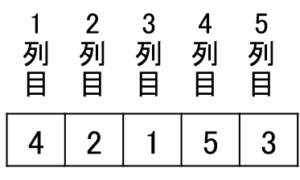
例えば「1列目4行目に1を書き入れる」と残りの2~5列目の4行目には1が書けませんから、ここで「1列目に4を選択する」と残りの2~5列目には4を選択できません。
あれれちょっと待ってください。どこかで見た問題と同じではないですか。
そう、5桁の整数問題(1~5の数字が書かれている5枚のカードを使って作ることのできる整数は何通り)にこの問題を置き換えることができる、とわかります。
答えは、5×4×3×2×1 = 120(通り)です。
「1~5を並べて5桁の整数を作る」というのは、「モデル化」です。
25のマス目の書き方は、5桁の数字と「1対1」に対応しています。
つまり、一見複雑そうに見える問題でも、「1対1」対応している、考え易いモデルに置き換えてやれば、簡単に解くことができます。
問題1~3で見てきたように、場合の数は、具体的に訊かれていることを一旦抽象化し、それを別の具体例で考えるとたちまち解けてしまうことがあります。
あなたも「センスがないから無理」と言わずに、うまいモデルを見つけることをキッカケに、いろいろ考えてみると、突破口が開けてきますよ。